数组中的逆序对

Problem description

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

Examples

Example 1:
Input: 1,2,3,4,5,6,7,0
Output: 7

Example 2:
Input: 7,6,5,4
Output: 5

Solution

完全没有思路，汗~
分治呀，分治呀，小伙计。

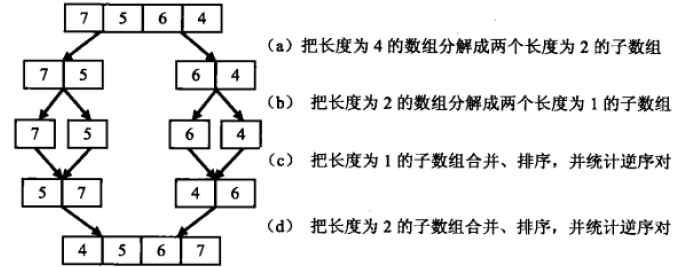
把数组分解为两个子数组，递归直至数组被拆分成两个为1的子数组。合并子数组同时统计逆序对。统计后需要将统计后的数组排序，防止统计重复。
嗨呀！这不就是归并大兄弟嘛，先求出左边已排好序的逆序数，再求出右边已排好序的逆序数，最后合并时求左右两组中的逆序数。
合并时需要注意归并排序的特征，在统计逆序数时，前面数组array[i] > 后面数组的array[j]时，那么因为左右两边均是有序数组。那么mid~j处的右侧数组数据必然都小于i。所以count += j - mid;
最后天杀的牛客哟，竟然数据会溢出，你放个Int返回值干啥

Code

 public int InversePairs(int[] array) {
    if (array == null || array.length == 0) {
        return 0;
    }

    int[] copy = new int[array.length];
    return mergeSort(array, copy, 0, array.length - 1);
}

public int mergeSort(int[] array, int[] copy, int low, int high) {
    if (low < high) {
        int length = (high - low) >> 1;
        int left = mergeSort(array, copy, low, low + length) % 1000000007;
        int right = mergeSort(array, copy, low + length + 1, high) % 1000000007;
        int mid = merge(array, copy, low, low + length, high) % 1000000007;
        return (left + right + mid) % 1000000007;
    }
    return 0;
}

private int merge(int[] array, int[] copy, int low, int mid, int high) {
    for (int i = low; i <= high; i++) {
        copy[i] = array[i];
    }
    int i = mid, j = high, k = high;
    int count = 0;
    while (i >= low && j > mid) {
        if (copy[i] > copy[j]) {
            array[k--] = copy[i--];
            count += j - mid;
            if (count >= 1000000007)//数值过大求余
            {
                count %= 1000000007;
            }
        } else {
            array[k--] = copy[j--];
        }
    }

    while (i >= low) {
        array[k--] = copy[i--];
    }
    while (j > mid) {
        array[k--] = copy[j--];
    }
    return count;
}