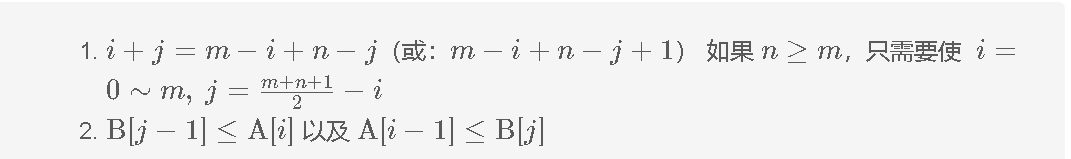Find the median of the two sorted arrays

Problem description

There are two sorted arrays nums1 and nums2 of size m and n respectively.Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).You may assume nums1 and nums2 cannot be both empty.

Examples

Example 1:
nums1 = [1, 3]
nums2 = [2]
The median is 2.0

Example 2:
nums1 = [1, 2]
nums2 = [3, 4]
The median is (2 + 3)/2 = 2.5

Solution

二分查找的思想

中位数是用来将一个集合划分为两个长度相等的子集，其中一个子集中的元素总是大于另一个子集中的元素。

1.两个长度相等的子集
2.一个子集中的元素总是大于另一个子集中的元素。

在这道题目中始终注意两个数组均为有序数组。

首先在任一位置 i 将A数组 划分成两个部分：

len(left_A)=i,len(right_A)=m−i.

注意：当 i = 0 时，left_A 为空集， 而当 i =m 时, right_A 为空集。

同理在任一位置 j 将B数组 划分成两个部分：

将left_A 和left_B 放入一个集合，并将 right_A 和right_B 放入另一个集合。 再把这两个新的集合分别命名为left_part 和right_part：

只要满足

1. len(left_part)=len(right_part)
2. max(left_part) < min(right_part)

要确保这两个条件，只需要保证：

我们可以按照以下步骤来进行二分查找保证B[j - 1] <= A[i] && A[i - 1] <= B[j]：
设 iMin = 0, iMax = m，在[iMin, iMax]中搜索
令i = (iMax + iMin) / 2, j = (m + n + 1) / 2 - i （保证len(left_part) = len(right_part) ）。接下来会遇到三种情况。

1. B[j - 1 ] <= A[i] && A[i - 1] <= B[j]时，找到对应i，j。
2. B[j - 1] > A[i]时，i小了， iMin = i + 1
3. A[i - 1] > B[j], iMax = i - 1

此外，难处理的就是边界问题，i = 0, i = m; j = 0, j = n.当 i, j 为临界值时，只需要判断B[j - 1] <= A[i] & A[i - 1] <= B[j]之中的一半即可。即i = 0时，A[i - 1]不存在，直接取B[j - 1] 即可.

如果数组长度 m + n 为奇数，直接返回结果即可，否则需要再找到右侧区域的最小值， 求平均值。
找右侧区域最小值也要注意边界啊，因为可能没有右侧区域了， i = m / j= n 时, 表明没有右侧区域，这时直接取另一半即可。如 i=m, 取 nums[j]

Code

class Solution {
        public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        if (nums1.length > nums2.length) {
            return findMedianSortedArrays(nums2, nums1);
        }
        int S1Len = nums1.length;
        int S2Len = nums2.length;
        int iMin = 0, iMax = S1Len, halfLen = (S1Len + S2Len + 1) / 2;
        while (iMin <= iMax) {
            int i = (iMin + iMax) / 2;
            int j = halfLen - i;
            if (i < iMax && nums1[i] < nums2[j - 1]) {
                iMin = i + 1;
            } else if (iMin < i && nums2[j] < nums1[i - 1]) {
                iMax = i - 1;
            } else {
                int maxLeft = 0;
                if (i == 0) {
                    maxLeft = nums2[j - 1];
                } else if (j == 0) {
                    maxLeft = nums1[i - 1];
                } else {
                    maxLeft = Math.max(nums1[i - 1], nums2[j - 1]);
                }
                if (((S1Len + S2Len) & 1) == 1) {
                    return maxLeft;
                }
                int minRight = 0;
                if (i == S1Len) {
                    minRight = nums2[j];
                } else if (j == S2Len) {
                    minRight = nums1[i];
                } else {
                    minRight = Math.min(nums1[i], nums2[j]);
                }
                return (maxLeft + minRight) / 2.0;
            }
        }
        return 0.0;
    }

}