Get water

Problem description

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

Examples

Example 1:
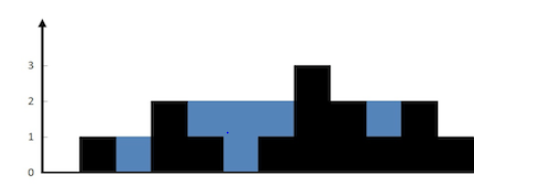
Input: [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6

Solution

　　这难道就是一看就懂，一写就懵逼的题目吗？一看就知道是木桶效应，嗯问题来了，咋写呢？ 苦思良久，还是看解析吧！ 发现博主和我想法不谋而合也是采取了木桶效应。取当前块的左右最大边界中的最低边界min.-当前块的高度。但这样做会超时。可以采用分治策略，先找到最高块高度和索引，分别计算左侧水面积和右侧水面积再相加。以计算左侧面积为例：判读当前块高度currentHeight是否大于maxHeight，为true的话，则累加（maxHeight - currentHeight ）;

Code

class Solution://Shortest barrel
   def trap(self, height):
       """
       :type height: List[int]
       :rtype: int
       """
       res, hei_len = 0, len(height)
       for i in range(1, hei_len-1):
           max_left, max_right = 0, 0
           for l in range(i+1):
               max_left = max(max_left, height[l])
           for r in range(i, hei_len):
               max_right = max(max_right, height[r])
               
           res += min(max_left, max_right) - height[i]
           
       return res

class Solution {
     public int trap(int[] height) {
        if (height.length == 0 || height.length == 1) {
            return 0;
        }
        int maxHeight = Integer.MIN_VALUE;
        int index = 0;
        for (int i = 0; i < height.length; i++) {
            if (height[i] > maxHeight) {
                maxHeight = height[i];
                index = i;
            }
        }

        int result = 0, currentMax = Integer.MIN_VALUE;

        for (int i = 0; i < index; i++) {
            if (currentMax >= height[i]) {
                result += currentMax - height[i];
            } else {
                currentMax = height[i];
            }
        }
        currentMax = Integer.MIN_VALUE;
        for (int i = height.length - 1; i > index; i--) {
            if (currentMax >= height[i]) {
                result += currentMax - height[i];
            } else {
                currentMax = height[i];
            }
        }
        return result;
    }

}